By Amir Jafari
Our floating industry is going bigger
The offshore wind turbine industry is developing larger wind turbines, and we need larger foundations to accommodate them in the oceans.
Floating offshore wind turbines will play a remarkable role in the future of the wind industry. Therefore, semisubmersibles, TLPs, spars and other floating concepts will be upscaled and become larger. Calculating the loads on these structures and the following platform responses is necessary to understand the behaviour of these floaters and develop them further.

Principal Power, WindFloat
How waves interact with floating structures
Offshore engineers are particularly interested in ocean waves and their interactions with floating platforms, as they have a major impact on these structures.
Hydrodynamic loads on the structures can be divided into two main categories:
1. Viscous loads
2. Non-viscous loads
Viscous loads are mainly drag, and the non-viscous loads include inertia terms.
For fixed-bottom offshore structures, we can use Morison’s equation to calculate drag and inertia using empirical measurements.
Considering a large floating structure, we need to note that the forces on the structure are dominated by inertia. Therefore, a refinement on Morison’s equation non-viscous loads is required to capture all the physical phenomena occuring.
An effort is made here to understand the non-viscous forces acting on a floating body.
Non-viscous wave loads on large-volume structures like semisubmersibles can be divided into two categories.
1. First-order linear wave-induced motion and loads
2. Second-order non-linear wave-induced motion and loads
First-order linear wave loads
We can superimpose regular waves to achieve an irregular sea state. As we do it linearly, we can linearly do the same for the resulting responses. This approach suggests that the linear motions and loads on the structure are harmonically oscillating with the same frequency as the wave loads on the system.
Considering an object in a wavefield is surrounded by moving water particles; therefore, this object is in a pressure field. By adding up the pressure acting on the body, we can calculate the linear loads affecting the body. This pressure on the body can be due to the incident wave and undisturbed wavefield (Froude-Krylov force), altered by the presence of the object (Diffraction) or created by the object’s motion itself (Radiation).
Froude-Krylov force
This force comes from the pressure distribution on the submerged surface of the structure due to approaching waves. To calculate this force, we assume the body is restrained from oscillating in the water (fixed), and the water is undisturbed. This hydrodynamic load is a part of the wave excitation loads. This is an inertia force which is proportional to the water acceleration.
Diffraction force
Consider the structure fixed, and the structure’s dimension is large comparing to the incident wavelength. The structure changes the form and distorts the incident wave field around itself; it has a scattering effect called diffraction or scattering force. This term represents the disturbance of the approaching waves by the restrained body.

Radiation forces
When considering a radiation force, the body is no longer considered fixed in the water; the structure has motion and oscillates at a given frequency. As opposed to diffracted waves, here we have no incident wave, and the motion of the structure generates waves; these waves produce a radiated force on the structure, i.e. water pressure on the body surface.
This force component is comprised of Added mass and Damping terms.
Added mass is the inertia of the water’s volume surrounding the body that moves with the structure’s motion. This component is in phase with the body acceleration.
Radiation damping is the force coming from the wave generated from the motion of the body and is in phase with the velocity of the body.
Froude-Krylov, diffraction and radiation forces can be calculated using the potential flow theory, which leads to the results in the form of load or displacement RAOs (Response Amplitude Operators) and added mass and damping matrices.
You can see the effect of diffraction and radiation in this video at minutes 2 and 3, respectively.
Second-order non-linear wave loads
First-order loads can sufficiently define the loads on the structure; however, for harsh sea states and the transitional motions of moored systems, including the second-order wave loads in calculations, can be essential. (Odd Magnus Faltinsen)
Here we consider the waves are approaching an oscillating body. Assume the superimposition of regular waves to make an irregular sea. These regular waves move at various frequencies, and the combination of these waves with different frequencies results in second-order wave loads.
These loads are proportional to the wave amplitudes squared. They are not in the wave frequency range and have either higher or lower frequencies, i.e. excitation by these loads is not in the range of wave frequency loads (Linear wave loads). Usually, they have a lower impact on the structure comparing the first-order wave loads. However, they excite different frequencies that can lead to resonance in the system and larger fatigue loads.
We can calculate the second-order loads using the Quadratic Transfer Function (QTF). This transfer function indicates the connection between the wave force and the combination of wave frequencies (3).
Mean wave drift force
If the regular waves have the same frequency, it results in a constant (zero frequency) contribution to the wave load called mean wave drift force. (See more Orinca.com). They are a constant load component responsible for the mean displacement of the floater. Various components contribute to the mean wave drift forces; however, the wave height is dominant. (For more information see Journée and Massie, W.W. 2001)
Difference frequency loads (Low-frequency)
These loads are also known as slow-varying wave drift forces. They have a frequency equal to the difference in frequencies between two waves.
As large floating structures like semisubmersibles have low frequencies in horizontal motions, i.e. surge and sway, the low-frequency drift forces can cause structural resonance, leading to large horizontal motion responses in these moored structures. If we do a full QTF analysis, the diagonal terms of the QTF matrix are mean drift, and the off-diagonal terms are slow drift forces (DNVGL-RP-0286, 2019, Coupled analysis of floating wind turbines.).
Sum frequency (High-frequency)
These waves have a frequency equal to the sum of the two wave frequencies. These forces are essential in TLPs due to high heave, roll and pitch frequencies. They can excite the resonance in the mentioned motions, i.e. ringing or springing, which leads to higher fatigue in tensioned mooring lines.
These are just some of the loads to consider
Additionally, we need to consider other hydrodynamic loads, such as current loads, to have a complete understanding of the loads on the floater and their corresponding integrated responses.
When I was doing my master’s at the University of Exeter, I wanted to think intuitively about the loads that we reviewed, which led to writing this article. It is just the starting point to work out the wave loads on the structure. To make what I said more clear, there is an excellent quote I once heard from across the room which it’s always stuck with me.
“Our job as offshore engineers is to capture which loads are relevant in a case-by-case situation, depending on the structure, area of interest and environmental conditions.”
So now let’s sit back and have a look at the figure below and consider what loads could be taken into account in different situations.
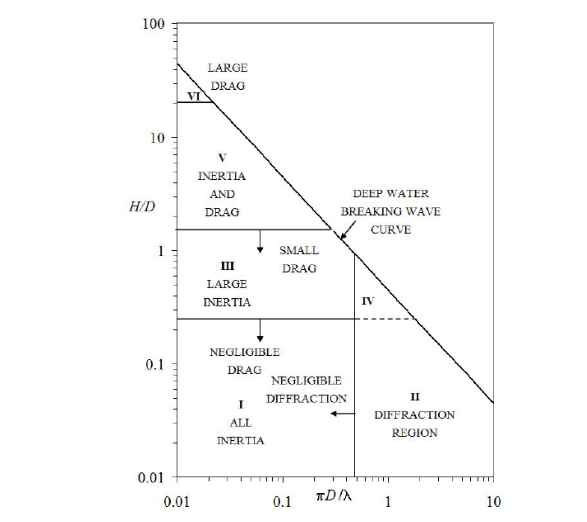
D = characterstic dimension
H = wave height
Limits of application for different structures (Chakrabarti)
Empire specialists can effectively and efficiently assist with your offshore wind project. To find out more, please Get in touch with the team at Empire Engineering.


